Euler Tour – Euler Trail – Hamiltonian Cycle all graph

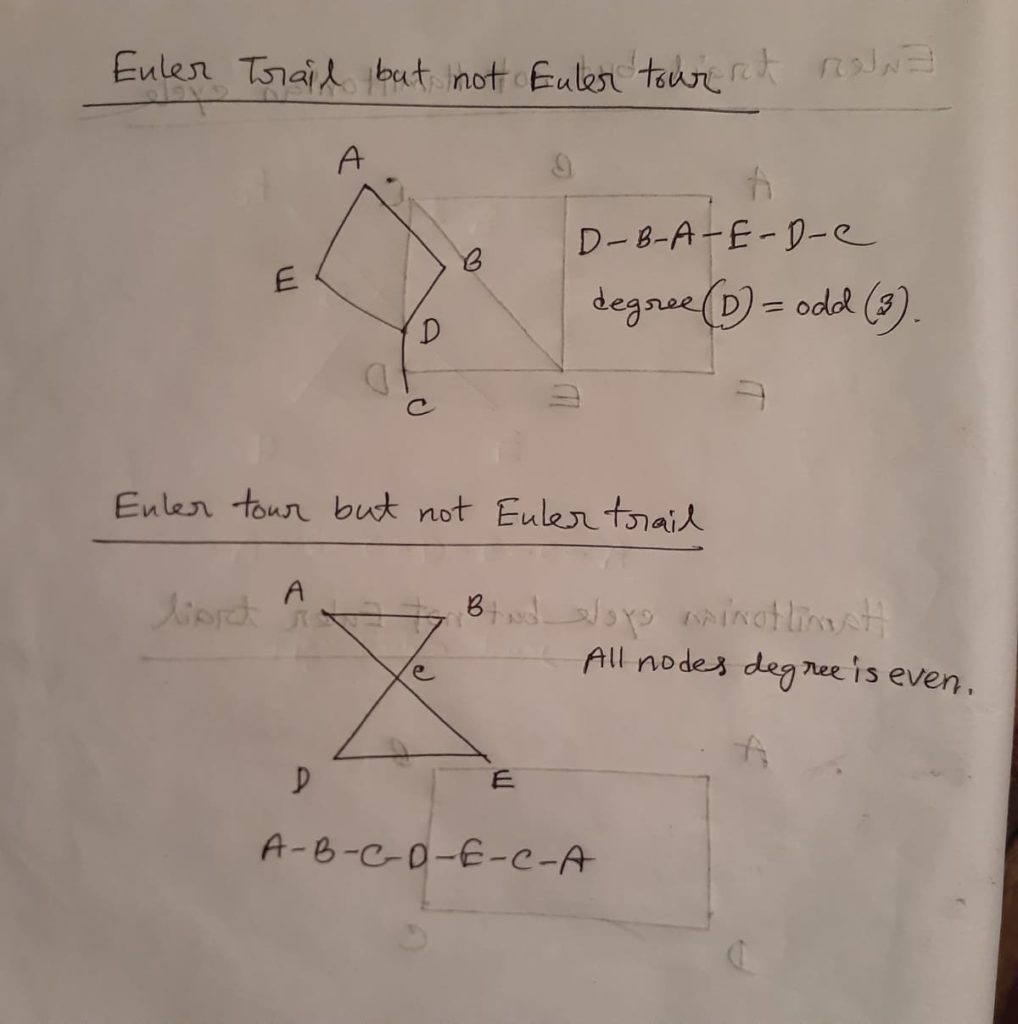
Euler Trail but not Euler Tour

Conditions:

1. At most 2 odd degree (number of odd degree <=2) of vertices.
2. Start and end nodes are different.

Euler Tour but not Euler Trail

Conditions:

1. All vertices have even degree.
2. Start and end node are same.

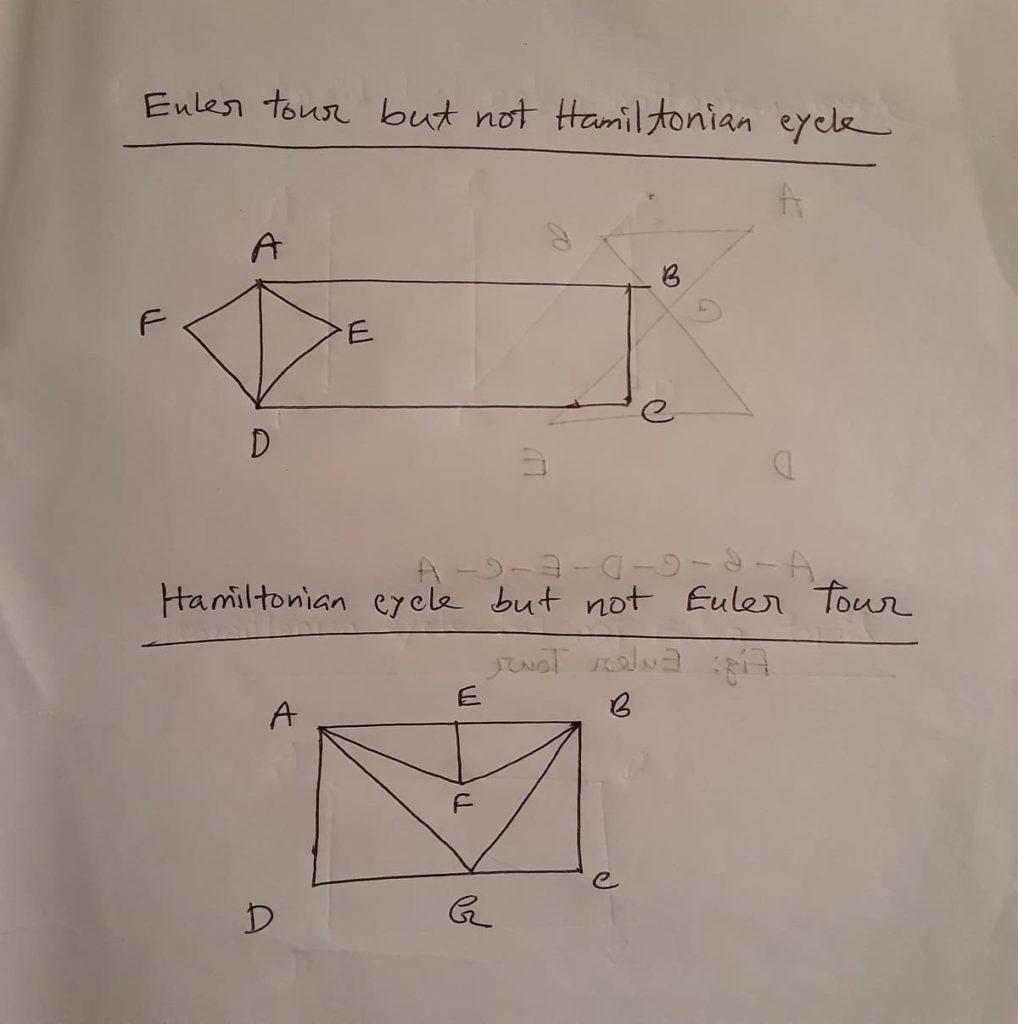
Euler Tour but not Hamiltonian cycle

Conditions:

1. All edges are traversed exactly once.
2. Some nodes (vertices) are traversed more than once.

Hamiltonian cycle but not Euler Tour

Conditions:

1. All nodes are traversed exactly once.
2. Some edges are traversed more than once.

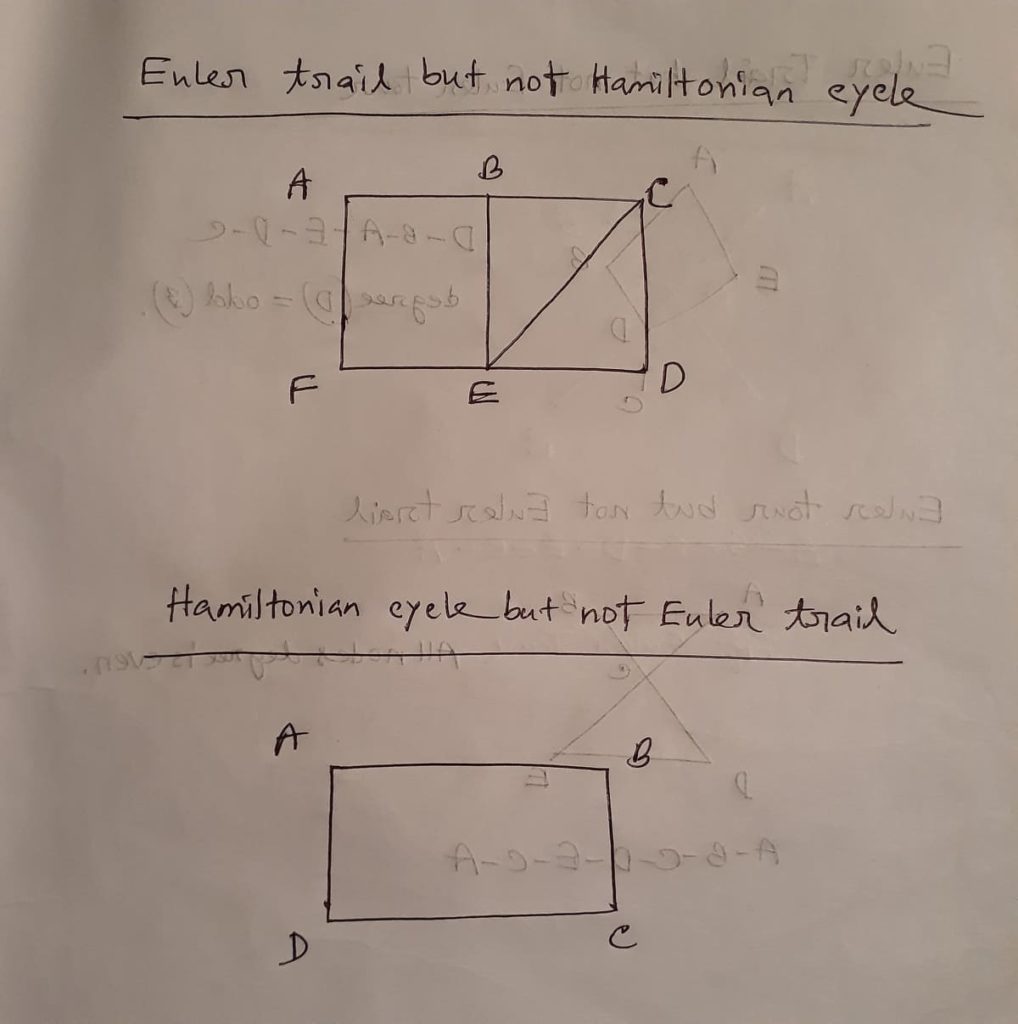
Euler Trail but not Hamiltonian cycle

Conditions:

1. Vertices have at most two odd degree.
2. Some nodes are traversed more than once.
3. Start and end node is not same.

Hamiltonian cycle but not Euler Trail

Conditions:

1. Start and end node is same.
2. Some edges is not traversed or no vertex has odd degree.

This graphs are very very important for any examinations.