Tree – Tree Properties and Minimum Spanning tree

Tree

A connected acyclic graph is called a tree.

Tree Properties

1. Any connected sub-graph is a tree.
2. There is a unique simple path between every pair of vertices.
3. Adding an edge between non-adjacent nodes in a tree creates a graph with a cycle.
4. Removing an edge disconnects the graph.
5. If the tree has at least two vertices, then it has at least two leaves.
6. The number of vertices in a tree is one larger than the number of edges.

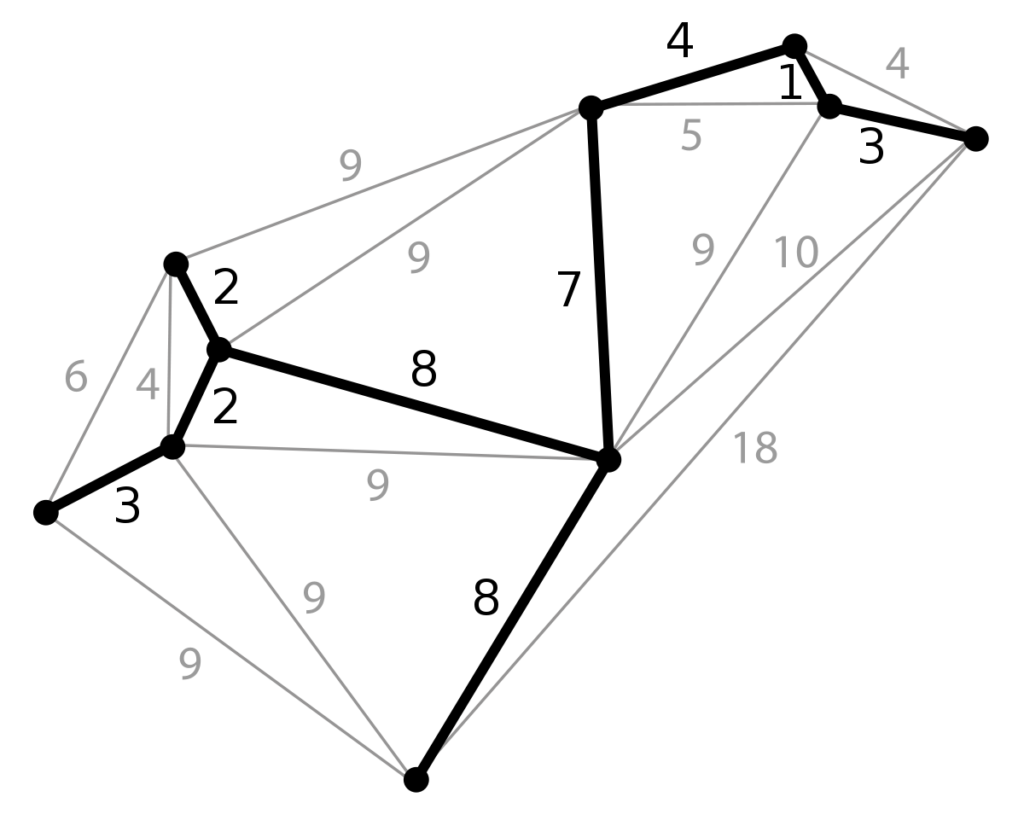
Minimum Spanning Tree (MST)

Spanning tree is a tree in a connected graph that contains a sub-graph with the same vertices as the graph. This is called a spanning tree for the graph. To find the spanning tree with minimum weight is called the minimum weight spanning tree (MST).

Fig: MST in a Graph