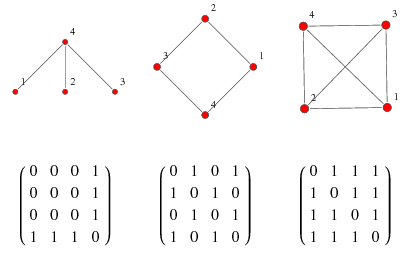
Adjacency Matrix and Incidence Matrix

Adjacency Matrix

An adjacency matrix is a sequence matrix used to represent a finite graph. It is a 2D array of size V X V matrix where V is the vertices of the graph. If nodes are connected with each other then we write 1 and if not connected then write 0 in adjacency matrix. If there exists any direction, then we have to flow with direction arrow only.

Fig: Adjacency Matrix

Incidence Matrix

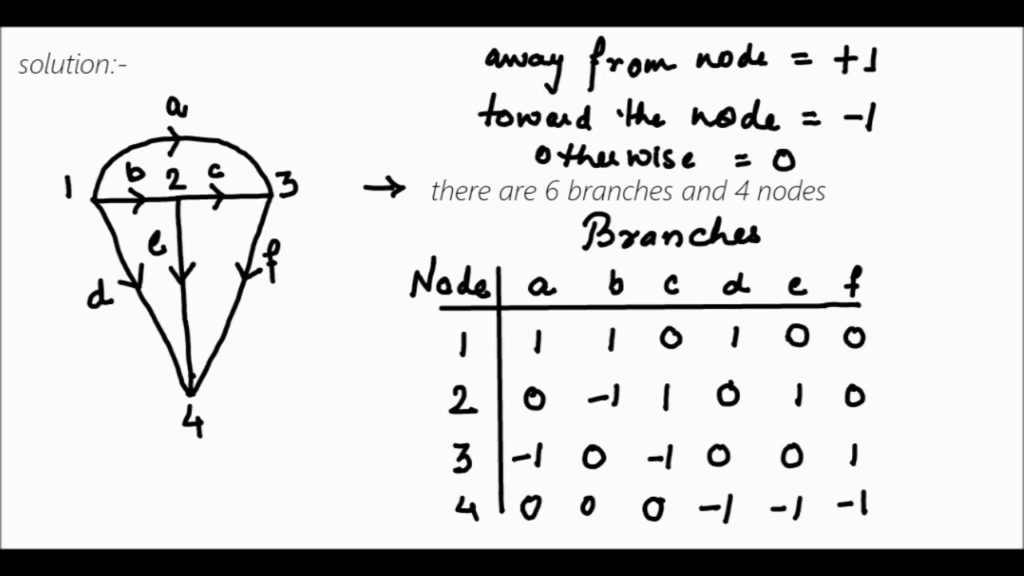
The incidence matrix of a graph that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related (called incident in this context) and 0 if they are not.

The rows are organized from nodes (Vertices) of the graphs and the columns are organized from the branches (Edges) of the graph. See an example below.

Fig: Incidence Matrix

Here, in the above matrix, away from the node denotes weight +1 and toward from the node denotes -1 weight and 0 otherwise.

Another example of incidence matrix

Fig: Incidence Matrix