Euler Tour – Euler Trail

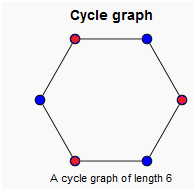
Cycle

In a graph, cycle is a tour with start and end with same node.

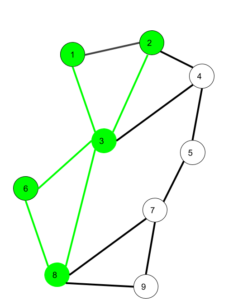
Trail

Trail is a path where every edge (line) is traversed exactly once and start and end vertices (node) are different.

Here 1->3->8->6->3->2 is trail and also 1->3->8->6->3->2->1 will be a closed trail.

 

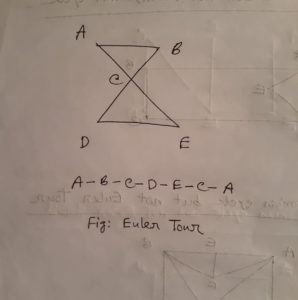
Euler Tour

Euler tour is a graph cycle when every edge is traversed exactly once but nodes (vertices) may be visited more than once and all vertices have even degree with start and end node is the same.

Fig: Euler Tour

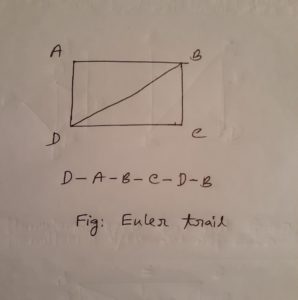
Euler Trail

Euler trail is a graph path when every edge is traversed exactly once but nodes (vertices) may be visited more than once and at most 2 vertices have odd degree with start and end node is the different.

Fig: Euler Trail